Math Primitives Definition¶
Common Attributes¶
Formal definition (auto-generated documentation based on XSD file).
All mathematical and physical elements have the following attributes in common:
- Id [xsd:ID] (optional) – Unique identifier of the element; used to reference elements
- Label [xsd:string] (optional) – Element label
- Description [xsd:string] (optional) – Element description
Strings¶
Formal definition (auto-generated documentation based on XSD file).
Strings are sequences of zero or more characters including tab, carriage return, line feed and unicode characters. See the XML Schema string datatype definition for more information.
Example:
“Pin 1”
<String>Pin 1</String>
Validation:
This type is validated using the XML Schema file.
Numbers¶
Simple Numbers¶
Formal definition (auto-generated documentation based on XSD file).
Decimal numbers can be defined using <SNumber>.
See the XML Schema decimal datatype definition for more information.
Example:
<SNumber>1.2</SNumber>
Validation:
This type is validated using the XML Schema file.
MathML Numbers¶
Formal definition (auto-generated documentation based on XSD file).
Other types of numbers can be represented using Strict Content MathML and OpenMath.
Note
Strict Content MathML elements are validated using the official RelaxNG schema via mpfo.nvdl.
The content of <MNumber> elements is validated using the Schematron schema mpfo.sch.
Integers¶
An integer is represented by an optional sign followed by a string of one or more decimal digits (Source).
Example:
<MNumber>
<mml:math>
<mml:cn type="integer">5</mml:cn>
</mml:math>
</MNumber>
Validation:
Attention
The content of <mml:cn> elements is currently not validated.
Rational Numbers¶
A rational number can be expressed as a quotient of two integers (Source).
Example:
<MNumber>
<mml:math>
<mml:apply>
<mml:csymbol cd="nums1">rational</mml:csymbol>
<mml:cn type="integer">4</mml:cn>
<mml:cn type="integer">5</mml:cn>
</mml:apply>
</mml:math>
</MNumber>
Validation:
This type is validated using the Schematron schema mpfo.sch which checks the structure of <mml:*> elements and that the second integer (denominator) is not zero.
Attention
The content of <mml:cn> elements is currently not validated (besides the mentioned test for zero).
Real Numbers¶
A real number consists of an optional sign (“+” or “-“) followed by a string of digits possibly separated into an integer and a fractional part by a decimal point (Source).
Example:
<MNumber>
<mml:math>
<mml:cn type="real">0.3</mml:cn>
</mml:math>
</MNumber>
Validation:
Attention
The content of <mml:cn> elements is currently not validated.
Double-Precision Floating-Point Numbers¶
MPFO allows the definition of floating-point numbers according to standard IEEE 754. This includes a subset of real numbers, \(-0\), \(+\infty\), \(-\infty\), and values for “not a number” (NaN) (Source 1, Source 2).
Example:
<MNumber>
<mml:math>
<mml:cn type="double">-1E4</mml:cn>
</mml:math>
</MNumber>
Other examples for valid numbers include: 1267.43233E12, 12.78e-2, 12, -0, 0, INF
The 64 bits of a double-precision floating-point number as prescribed by IEEE 754 may also be written as 16 digit hexadecimal number (Source).
Example:
<MNumber>
<mml:math>
<mml:cn type="hexdouble">0x7F800000</mml:cn>
</mml:math>
</MNumber>
Validation:
Attention
The content of <mml:cn> elements is currently not validated.
Complex Numbers¶
A complex number is represented by two real numbers: the real part and the imaginary part (Source).
Example:
<MNumber>
<mml:math>
<mml:apply>
<mml:csymbol cd="complex1">complex_cartesian</mml:csymbol>
<mml:cn type="real">3.2</mml:cn>
<mml:cn type="real">1.6</mml:cn>
</mml:apply>
</mml:math>
</MNumber>
Validation:
Attention
The content of <mml:cn> elements is currently not validated.
Tolerances¶
Formal definition (auto-generated documentation based on XSD file).
Tolerances define the acceptable deviation from a nominal value and comprise a lower and upper bound. Each bound may be an absolute value or relative to the nominal value.
Every <Tolerance> element must contain one <LowerBound> and one <UpperBound> element.
They have one mandatory attribute BoundType which is either “absolute” or “relative” and contain either one <SNumber> or one <MNumber> element.
Example:
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.1</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.1</SNumber>
</UpperBound>
</Tolerance>
Example:
<Tolerance>
<LowerBound BoundType="relative">
<SNumber>0</SNumber>
</LowerBound>
<UpperBound BoundType="relative">
<SNumber>0.05</SNumber>
</UpperBound>
</Tolerance>
Validation:
This type is validated using the XML Schema file.
Attention
See Simple Numbers and MathML Numbers for details about <SNumber> and <MNumber> element validation.
Toleranced Numbers¶
Formal definition (auto-generated documentation based on XSD file).
A toleranced number consists of a number and a tolerance.
The number can be specified using <SNumber> or <MNumber> (see Simple Numbers and MathML Numbers for details).
Example:
<TolerancedNumber>
<SNumber>1.5</SNumber>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.1</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.1</SNumber>
</UpperBound>
</Tolerance>
</TolerancedNumber>
Validation:
This type is validated using the XML Schema file.
Attention
See Simple Numbers and MathML Numbers for details about <SNumber> and <MNumber> element validation.
Units¶
Formal definition (auto-generated documentation based on XSD file).
Units are represented using Strict Content MathML and OpenMath.
Note
Strict Content MathML elements are validated using the official RelaxNG schema via mpfo.nvdl.
Attention
Content dictionaries and their entries are currently not validated.
Simple Units¶
Simple units comprise a single unit from one of the OpenMath content dictionaries without a prefix.
Example:
meter (m)
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">metre</mml:csymbol>
</mml:math>
</Unit>
Prefixes¶
Unit prefixes are defined by applying the prefix operator from the units_ops1 content dictionary to a prefix from the units_siprefix1 content dictionary and a simple unit.
Supported prefixes: atto, centi, deci, deka, exa, femto, giga, hecto, kilo, mega, micro, milli, nano, peta, pico, tera, yocto, yotta, zepto, zetta
Example:
kilometre (km)
<Unit>
<mml:math>
<mml:apply>
<mml:csymbol cd="units_ops1">prefix</mml:csymbol>
<mml:csymbol cd="units_siprefix1">kilo</mml:csymbol>
<mml:csymbol cd="SI_BaseUnits1">metre</mml:csymbol>
</mml:apply>
</mml:math>
</Unit>
Compound Units¶
Compound units are formed by powers, products or quotients of simple units. The arith1 content dictionary contains the relevant arithmetic functions.
Example:
newton metre (N m)
<Unit>
<mml:math>
<mml:apply>
<mml:csymbol cd="arith1">times</mml:csymbol>
<mml:csymbol cd="SI_NamedDerivedUnits1">newton</mml:csymbol>
<mml:csymbol cd="SI_BaseUnits1">metre</mml:csymbol>
</mml:apply>
</mml:math>
</Unit>
Example:
cubic metre (m³)
<Unit>
<mml:math>
<mml:apply>
<mml:csymbol cd="arith1">power</mml:csymbol>
<mml:csymbol cd="SI_BaseUnits1">metre</mml:csymbol>
<mml:cn type="integer">3</mml:cn>
</mml:apply>
</mml:math>
</Unit>
Example:
litre per 100 km (l/100 km)
<Unit>
<mml:math>
<mml:apply>
<mml:csymbol cd="arith1">divide</mml:csymbol>
<mml:csymbol cd="SIUsed_OffSystemUnits1">litre</mml:csymbol>
<mml:apply>
<mml:csymbol cd="arith1">times</mml:csymbol>
<mml:cn type="integer">100</mml:cn>
<mml:apply>
<mml:csymbol cd="units_ops1">prefix</mml:csymbol>
<mml:csymbol cd="units_siprefix1">kilo</mml:csymbol>
<mml:csymbol cd="SI_BaseUnits1">metre</mml:csymbol>
</mml:apply>
</mml:apply>
</mml:apply>
</mml:math>
</Unit>
Supported Units¶
OpenMath defines units in multiple content dictionaries.
| Content dictionary | Selection of supported units |
|---|---|
| SI_BaseUnits1 | ampere, candela, kelvin, kilogram, metre, mole, one (dimensionless), second |
| SI_NamedDerivedUnits1 | becquerel, coulomb, degree celsius, farad, gram, gray, henry, hertz, joule, katal, lumen, lux, newton, ohm, pascal, radian, siemens, sievert, steradian, tesla, volt, watt, weber |
| SIUsed_OffSystemUnits1 | bel, day, degree of arc, hour, litre, minute, minute of arc, neper, second of arc, tonne |
| units_time1 | calendar_month, calendar_year, week |
Quantities¶
Formal definition (auto-generated documentation based on XSD file).
A quantity consists of a number and a unit.
Example:
4.4 litre per 100 km (4.4 l/100 km)
<Quantity>
<SNumber>4.4</SNumber>
<Unit>
<mml:math>
<mml:apply>
<mml:csymbol cd="arith1">divide</mml:csymbol>
<mml:csymbol cd="SIUsed_OffSystemUnits1">litre</mml:csymbol>
<mml:apply>
<mml:csymbol cd="arith1">times</mml:csymbol>
<mml:cn type="integer">100</mml:cn>
<mml:apply>
<mml:csymbol cd="units_ops1">prefix</mml:csymbol>
<mml:csymbol cd="units_siprefix1">kilo</mml:csymbol>
<mml:csymbol cd="SI_BaseUnits1">metre</mml:csymbol>
</mml:apply>
</mml:apply>
</mml:apply>
</mml:math>
</Unit>
</Quantity>
Validation:
This type is validated using the XML Schema file.
Toleranced Quantities¶
Formal definition (auto-generated documentation based on XSD file).
A toleranced quantity consists of a number, a tolerance and a unit.
Example:
(4.4 \(\pm\) 1.0) litre per 100 km ((4.4 \(\pm\) 1.0) l/100 km)
<TolerancedQuantity>
<SNumber>4.4</SNumber>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>1.0</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>1.0</SNumber>
</UpperBound>
</Tolerance>
<Unit>
<mml:math>
<mml:apply>
<mml:csymbol cd="arith1">divide</mml:csymbol>
<mml:csymbol cd="SIUsed_OffSystemUnits1">litre</mml:csymbol>
<mml:apply>
<mml:csymbol cd="arith1">times</mml:csymbol>
<mml:cn type="integer">100</mml:cn>
<mml:apply>
<mml:csymbol cd="units_ops1">prefix</mml:csymbol>
<mml:csymbol cd="units_siprefix1">kilo</mml:csymbol>
<mml:csymbol cd="SI_BaseUnits1">metre</mml:csymbol>
</mml:apply>
</mml:apply>
</mml:apply>
</mml:math>
</Unit>
</TolerancedQuantity>
Validation:
This type is validated using the XML Schema file.
Attention
See Numbers, Tolerances, and Units for details about validation of <SNumber>, <MNumber>, <Tolerance>, and <Unit> elements.
Intervals¶
An interval defines a set of numbers or quantities between a lower endpoint and an upper endpoint.
Every <*Interval> element must contain one <LowerBound> and one <UpperBound> element.
They have one mandatory attribute BoundType which is either “open” (interval does not include the endpoint) or “closed” (interval includes the endpoint).
Number Intervals¶
Formal definition (auto-generated documentation based on XSD file).
Number intervals have endpoints that are either <SNumber> or <MNumber> elements.
Example:
(1.0, 10.0) (open interval that does not include its endpoints)
<NumberInterval>
<LowerBound BoundType="open">
<SNumber>1.0</SNumber>
</LowerBound>
<UpperBound BoundType="open">
<SNumber>10.0</SNumber>
</UpperBound>
</NumberInterval>
Example:
[1.0, 10.0] (closed interval that does include its endpoints)
<NumberInterval>
<LowerBound BoundType="closed">
<SNumber>1.0</SNumber>
</LowerBound>
<UpperBound BoundType="closed">
<SNumber>10.0</SNumber>
</UpperBound>
</NumberInterval>
Validation:
This type is validated using the XML Schema file.
Attention
See Simple Numbers and MathML Numbers for details about <SNumber> and <MNumber> element validation.
Toleranced Number Intervals¶
Formal definition (auto-generated documentation based on XSD file).
Toleranced number intervals have endpoints that are <TolerancedNumber> elements.
Example:
<TolerancedNumberInterval>
<LowerBound BoundType="closed">
<TolerancedNumber>
<SNumber>1.0</SNumber>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.1</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.1</SNumber>
</UpperBound>
</Tolerance>
</TolerancedNumber>
</LowerBound>
<UpperBound BoundType="closed">
<TolerancedNumber>
<SNumber>10.0</SNumber>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.1</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.1</SNumber>
</UpperBound>
</Tolerance>
</TolerancedNumber>
</UpperBound>
</TolerancedNumberInterval>
This type is validated using the XML Schema file.
Attention
See Toleranced Numbers for details about <TolerancedNumber> element validation.
Quantity Intervals¶
Formal definition (auto-generated documentation based on XSD file).
Quantity intervals have endpoints that are <Quantity> elements.
Example:
<QuantityInterval>
<LowerBound BoundType="closed">
<Quantity>
<SNumber>1.0</SNumber>
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">metre</mml:csymbol>
</mml:math>
</Unit>
</Quantity>
</LowerBound>
<UpperBound BoundType="closed">
<Quantity>
<SNumber>10.0</SNumber>
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">metre</mml:csymbol>
</mml:math>
</Unit>
</Quantity>
</UpperBound>
</QuantityInterval>
This type is validated using the XML Schema file.
Attention
See Quantities for details about <Quantity> element validation.
Toleranced Quantity Intervals¶
Formal definition (auto-generated documentation based on XSD file).
Toleranced quantity intervals have endpoints that are <TolerancedQuantity> elements.
<TolerancedQuantityInterval>
<LowerBound BoundType="closed">
<TolerancedQuantity>
<SNumber>1.0</SNumber>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.1</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.1</SNumber>
</UpperBound>
</Tolerance>
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">metre</mml:csymbol>
</mml:math>
</Unit>
</TolerancedQuantity>
</LowerBound>
<UpperBound BoundType="closed">
<TolerancedQuantity>
<SNumber>10.0</SNumber>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.1</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.1</SNumber>
</UpperBound>
</Tolerance>
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">metre</mml:csymbol>
</mml:math>
</Unit>
</TolerancedQuantity>
</UpperBound>
</TolerancedQuantityInterval>
This type is validated using the XML Schema file.
Attention
See Toleranced Quantities for details about <TolerancedQuantity> element validation.
Vectors¶
Vectors are ordered lists of elements.
String Vectors¶
Formal definition (auto-generated documentation based on XSD file).
A string vector consists of one or more Strings.
Example:
<StringVector>
<String>Pin 1</String>
<String>Pin 2</String>
<String>Pin 3</String>
</StringVector>
Validation:
This type is validated using the XML Schema file.
Number Vectors¶
Formal definition (auto-generated documentation based on XSD file).
A number vector consists of one or more Numbers.
It may contain both, <SNumber> and <MNumber> elements.
Example:
<NumberVector>
<SNumber>1.0</SNumber>
<SNumber>1.5</SNumber>
<SNumber>2.0</SNumber>
</NumberVector>
Validation:
This type is validated using the XML Schema file.
Attention
See Simple Numbers and MathML Numbers for details about <SNumber> and <MNumber> element validation.
Number Interval Vectors¶
Formal definition (auto-generated documentation based on XSD file).
A number interval vector consists of one or more Number Intervals.
Example:
<NumberIntervalVector>
<NumberInterval>
<LowerBound BoundType="closed">
<SNumber>0.0</SNumber>
</LowerBound>
<UpperBound BoundType="closed">
<SNumber>1.0</SNumber>
</UpperBound>
</NumberInterval>
<NumberInterval>
<LowerBound BoundType="closed">
<SNumber>0.0</SNumber>
</LowerBound>
<UpperBound BoundType="closed">
<SNumber>1.5</SNumber>
</UpperBound>
</NumberInterval>
<NumberInterval>
<LowerBound BoundType="closed">
<SNumber>0.0</SNumber>
</LowerBound>
<UpperBound BoundType="closed">
<SNumber>2.0</SNumber>
</UpperBound>
</NumberInterval>
</NumberIntervalVector>
Validation:
This type is validated using the XML Schema file.
Attention
See Number Intervals for details about <NumberInterval> element validation.
Tolerance Vectors¶
Formal definition (auto-generated documentation based on XSD file).
A tolerance vector consists of one or more Tolerances.
Example:
<ToleranceVector>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.1</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.1</SNumber>
</UpperBound>
</Tolerance>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.15</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.15</SNumber>
</UpperBound>
</Tolerance>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.2</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.2</SNumber>
</UpperBound>
</Tolerance>
</ToleranceVector>
Validation:
This type is validated using the XML Schema file.
Attention
See Tolerances for details about <Tolerance> element validation.
Toleranced Number Vectors¶
Formal definition (auto-generated documentation based on XSD file).
Vectors of toleranced numbers comprise a number vector (or sparse number vector) and a tolerance vector (or sparse tolerance vector). If all tolerances are equal, a single tolerance may be used instead of a vector.
Example:
<TolerancedNumberVector>
<NumberVector>
<SNumber>1.0</SNumber>
<SNumber>1.5</SNumber>
<SNumber>2.0</SNumber>
</NumberVector>
<ToleranceVector>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.1</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.1</SNumber>
</UpperBound>
</Tolerance>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.15</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.15</SNumber>
</UpperBound>
</Tolerance>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.2</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.2</SNumber>
</UpperBound>
</Tolerance>
</ToleranceVector>
</TolerancedNumberVector>
Example:
<TolerancedNumberVector>
<NumberVector>
<SNumber>1.0</SNumber>
<SNumber>1.5</SNumber>
<SNumber>2.0</SNumber>
</NumberVector>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.1</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.1</SNumber>
</UpperBound>
</Tolerance>
</TolerancedNumberVector>
Validation:
This type is validated using the XML Schema file.
The Schematron schema file checks that <NumberVector> and <ToleranceVector> have the same number of child elements.
Attention
See Number Vectors, Tolerance Vectors, and Tolerances for details about <NumberVector>, <ToleranceVector>, and <Tolerance> element validation.
Unit Vectors¶
Formal definition (auto-generated documentation based on XSD file).
A unit vector consists of one or more Units.
Example:
<UnitVector>
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">metre</mml:csymbol>
</mml:math>
</Unit>
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">second</mml:csymbol>
</mml:math>
</Unit>
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">gram</mml:csymbol>
</mml:math>
</Unit>
</UnitVector>
Validation:
This type is validated using the XML Schema file.
Attention
See Units for details about <Unit> element validation.
Quantity Vectors¶
Formal definition (auto-generated documentation based on XSD file).
Quantity vectors comprise a number vector (or sparse number vector) and a unit vector (or sparse unit vector). If all quantities have the same unit, a single unit may be used instead of a vector.
Example:
<QuantityVector>
<NumberVector>
<SNumber>1.0</SNumber>
<SNumber>1.5</SNumber>
<SNumber>2.0</SNumber>
</NumberVector>
<UnitVector>
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">metre</mml:csymbol>
</mml:math>
</Unit>
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">second</mml:csymbol>
</mml:math>
</Unit>
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">gram</mml:csymbol>
</mml:math>
</Unit>
</UnitVector>
</QuantityVector>
Example:
<QuantityVector>
<NumberVector>
<SNumber>1.0</SNumber>
<SNumber>1.5</SNumber>
<SNumber>2.0</SNumber>
</NumberVector>
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">metre</mml:csymbol>
</mml:math>
</Unit>
</QuantityVector>
Validation:
This type is validated using the XML Schema file.
The Schematron schema file checks that <NumberVector> and <UnitVector> have the same number of child elements.
Attention
See Number Vectors, Unit Vectors, and Units for details about <NumberVector>, <UnitVector>, and <Unit> element validation.
Toleranced Quantity Vectors¶
Formal definition (auto-generated documentation based on XSD file).
Vectors of toleranced quantities comprise a number vector (or sparse number vector), a tolerance vector (or sparse tolerance vector), and a unit vector (or sparse unit vector). If all quantities have the same tolerance/unit, a single tolerance/unit may be used instead of a vector.
Example:
<TolerancedQuantityVector>
<NumberVector>
<SNumber>1.0</SNumber>
<SNumber>1.5</SNumber>
<SNumber>2.0</SNumber>
</NumberVector>
<ToleranceVector>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.1</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.1</SNumber>
</UpperBound>
</Tolerance>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.15</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.15</SNumber>
</UpperBound>
</Tolerance>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.2</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.2</SNumber>
</UpperBound>
</Tolerance>
</ToleranceVector>
<UnitVector>
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">metre</mml:csymbol>
</mml:math>
</Unit>
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">second</mml:csymbol>
</mml:math>
</Unit>
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">gram</mml:csymbol>
</mml:math>
</Unit>
</UnitVector>
</TolerancedQuantityVector>
Example:
<TolerancedQuantityVector>
<NumberVector>
<SNumber>1.0</SNumber>
<SNumber>1.5</SNumber>
<SNumber>2.0</SNumber>
</NumberVector>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.1</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.1</SNumber>
</UpperBound>
</Tolerance>
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">metre</mml:csymbol>
</mml:math>
</Unit>
</TolerancedQuantityVector>
Validation:
This type is validated using the XML Schema file.
The Schematron schema file checks that <NumberVector>, <ToleranceVector>, and <UnitVector> have the same number of child elements.
Attention
See Number Vectors, Tolerance Vectors, Unit Vectors, Tolerances, and Units for details about <NumberVector>, <ToleranceVector>, <UnitVector>, <Tolerance> and <Unit> element validation.
Sparse Vectors¶
Just like normal vectors, sparse vectors are ordered list of elements. In a sparse vector, most elements have the same value. Therefore, for each sparse vector, a default value is specified, as well as all elements that are not equal to this default value.
All types of sparse vectors share the same structure:
- Attributes:
- ElementCount [xsd:positiveInteger] – number of elements in the sparse vector
- DefaultElement – default element
- element (by value or by reference)
- Elements
- Element (1..∞):
- Attributes:
- Index [xsd:positiveInteger] – one-based index of the element
- element (by value or by reference)
Sparse String Vectors¶
Formal definition (auto-generated documentation based on XSD file).
A sparse string vector consists of one or more Strings.
Example:
<StringSparseVector ElementCount="3">
<DefaultElement>
<String>Vdd</String>
</DefaultElement>
<Elements>
<Element Index="3">
<String>Vss</String>
</Element>
</Elements>
</StringSparseVector>
Validation:
This type is validated using the XML Schema file.
Sparse Number Vectors¶
Formal definition (auto-generated documentation based on XSD file).
A sparse number vector consists of one or more Numbers.
It may contain both, <SNumber> and <MNumber> elements.
Example:
<NumberSparseVector ElementCount="3">
<DefaultElement>
<SNumber>1.0</SNumber>
</DefaultElement>
<Elements>
<Element Index="3">
<SNumber>2.0</SNumber>
</Element>
</Elements>
</NumberSparseVector>
Validation:
This type is validated using the XML Schema file.
Attention
See Simple Numbers and MathML Numbers for details about <SNumber> and <MNumber> element validation.
Sparse Tolerance Vectors¶
Formal definition (auto-generated documentation based on XSD file).
A sparse tolerance vector consists of one or more Tolerances.
Example:
<ToleranceSparseVector ElementCount="3">
<DefaultElement>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.1</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.1</SNumber>
</UpperBound>
</Tolerance>
</DefaultElement>
<Elements>
<Element Index="3">
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.2</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.2</SNumber>
</UpperBound>
</Tolerance>
</Element>
</Elements>
</ToleranceSparseVector>
Validation:
This type is validated using the XML Schema file.
Attention
See Tolerances for details about <Tolerance> element validation.
Sparse Toleranced Number Vectors¶
Formal definition (auto-generated documentation based on XSD file).
A sparse toleranced number vector consists of one or more Toleranced Numbers.
Example:
<TolerancedNumberSparseVector ElementCount="3">
<DefaultElement>
<TolerancedNumber>
<SNumber>1.0</SNumber>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.1</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.1</SNumber>
</UpperBound>
</Tolerance>
</TolerancedNumber>
</DefaultElement>
<Elements>
<Element Index="3">
<TolerancedNumber>
<SNumber>2.0</SNumber>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.2</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.2</SNumber>
</UpperBound>
</Tolerance>
</TolerancedNumber>
</Element>
</Elements>
</TolerancedNumberSparseVector>
Validation:
This type is validated using the XML Schema file.
Attention
See Toleranced Numbers for details about <TolerancedNumber> element validation.
Sparse Unit Vectors¶
Formal definition (auto-generated documentation based on XSD file).
A sparse unit vector consists of one or more Units.
Example:
<UnitSparseVector ElementCount="3">
<DefaultElement>
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">metre</mml:csymbol>
</mml:math>
</Unit>
</DefaultElement>
<Elements>
<Element Index="3">
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">gram</mml:csymbol>
</mml:math>
</Unit>
</Element>
</Elements>
</UnitSparseVector>
Validation:
This type is validated using the XML Schema file.
Attention
See Units for details about <Unit> element validation.
Sparse Quantity Vectors¶
Formal definition (auto-generated documentation based on XSD file).
A sparse quantity vector consists of one or more Quantities.
Example:
<QuantitySparseVector ElementCount="3">
<DefaultElement>
<Quantity>
<SNumber>1.0</SNumber>
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">metre</mml:csymbol>
</mml:math>
</Unit>
</Quantity>
</DefaultElement>
<Elements>
<Element Index="3">
<Quantity>
<SNumber>2.0</SNumber>
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">gram</mml:csymbol>
</mml:math>
</Unit>
</Quantity>
</Element>
</Elements>
</QuantitySparseVector>
Validation:
This type is validated using the XML Schema file.
Attention
See Quantities for details about <Quantity> element validation.
Sparse Toleranced Quantity Vectors¶
Formal definition (auto-generated documentation based on XSD file).
A sparse vector of toleranced quantities consists of Toleranced Quantities.
Example:
<TolerancedQuantitySparseVector ElementCount="3">
<DefaultElement>
<TolerancedQuantity>
<SNumber>1.0</SNumber>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.1</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.1</SNumber>
</UpperBound>
</Tolerance>
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">metre</mml:csymbol>
</mml:math>
</Unit>
</TolerancedQuantity>
</DefaultElement>
<Elements>
<Element Index="3">
<TolerancedQuantity>
<SNumber>2.0</SNumber>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.2</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.2</SNumber>
</UpperBound>
</Tolerance>
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">gram</mml:csymbol>
</mml:math>
</Unit>
</TolerancedQuantity>
</Element>
</Elements>
</TolerancedQuantitySparseVector>
Validation:
This type is validated using the XML Schema file.
Attention
See Toleranced Quantities for details about <TolerancedQuantity> element validation.
Matrices¶
Matrices are 2-dimensional arrays of elements. They consist of one or more matrix rows, each of which contains one or more elements.
Note
The Schematron schema file checks that all rows of a matrix have the same number of child elements.
String Matrices¶
Formal definition (auto-generated documentation based on XSD file).
A string matrix consists of one or more rows of Strings.
Example:
<StringMatrix>
<StringMatrixRow>
<String>Pin 11</String>
<String>Pin 12</String>
</StringMatrixRow>
<StringMatrixRow>
<String>Pin 21</String>
<String>Pin 22</String>
</StringMatrixRow>
<StringMatrixRow>
<String>Pin 31</String>
<String>Pin 32</String>
</StringMatrixRow>
</StringMatrix>
Validation:
This type is validated using the XML Schema file.
Number Matrices¶
Formal definition (auto-generated documentation based on XSD file).
A number matrix consists of one or more rows of Numbers.
Each row may contain both, <SNumber> and <MNumber> elements.
Example:
<NumberMatrix>
<NumberMatrixRow>
<SNumber>1.0</SNumber>
<SNumber>2.0</SNumber>
</NumberMatrixRow>
<NumberMatrixRow>
<SNumber>1.5</SNumber>
<SNumber>3.0</SNumber>
</NumberMatrixRow>
<NumberMatrixRow>
<SNumber>2.0</SNumber>
<SNumber>4.0</SNumber>
</NumberMatrixRow>
</NumberMatrix>
Validation:
This type is validated using the XML Schema file.
Attention
See Simple Numbers and MathML Numbers for details about <SNumber> and <MNumber> element validation.
Tolerance Matrices¶
Formal definition (auto-generated documentation based on XSD file).
A tolerance matrix consists of one or more rows of Tolerances.
Example:
<ToleranceMatrix>
<ToleranceMatrixRow>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.1</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.1</SNumber>
</UpperBound>
</Tolerance>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.2</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.2</SNumber>
</UpperBound>
</Tolerance>
</ToleranceMatrixRow>
<ToleranceMatrixRow>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.15</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.15</SNumber>
</UpperBound>
</Tolerance>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.3</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.3</SNumber>
</UpperBound>
</Tolerance>
</ToleranceMatrixRow>
<ToleranceMatrixRow>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.2</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.2</SNumber>
</UpperBound>
</Tolerance>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.4</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.4</SNumber>
</UpperBound>
</Tolerance>
</ToleranceMatrixRow>
</ToleranceMatrix>
Validation:
This type is validated using the XML Schema file.
Attention
See Tolerances for details about <Tolerance> element validation.
Toleranced Number Matrices¶
Formal definition (auto-generated documentation based on XSD file).
Matrices of toleranced numbers comprise a number matrix (or sparse number matrix) and a tolerance matrix (or sparse tolerance matrix). If all tolerances are equal, a single tolerance may be used instead of a matrix.
Example:
<TolerancedNumberMatrix>
<NumberMatrix>
<NumberMatrixRow>
<SNumber>1.0</SNumber>
<SNumber>2.0</SNumber>
</NumberMatrixRow>
<NumberMatrixRow>
<SNumber>1.5</SNumber>
<SNumber>3.0</SNumber>
</NumberMatrixRow>
<NumberMatrixRow>
<SNumber>2.0</SNumber>
<SNumber>4.0</SNumber>
</NumberMatrixRow>
</NumberMatrix>
<ToleranceMatrix>
<ToleranceMatrixRow>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.1</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.1</SNumber>
</UpperBound>
</Tolerance>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.2</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.2</SNumber>
</UpperBound>
</Tolerance>
</ToleranceMatrixRow>
<ToleranceMatrixRow>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.15</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.15</SNumber>
</UpperBound>
</Tolerance>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.3</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.3</SNumber>
</UpperBound>
</Tolerance>
</ToleranceMatrixRow>
<ToleranceMatrixRow>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.2</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.2</SNumber>
</UpperBound>
</Tolerance>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.4</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.4</SNumber>
</UpperBound>
</Tolerance>
</ToleranceMatrixRow>
</ToleranceMatrix>
</TolerancedNumberMatrix>
Example:
<TolerancedNumberMatrix>
<NumberMatrix>
<NumberMatrixRow>
<SNumber>1.0</SNumber>
<SNumber>2.0</SNumber>
</NumberMatrixRow>
<NumberMatrixRow>
<SNumber>1.5</SNumber>
<SNumber>3.0</SNumber>
</NumberMatrixRow>
<NumberMatrixRow>
<SNumber>2.0</SNumber>
<SNumber>4.0</SNumber>
</NumberMatrixRow>
</NumberMatrix>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.1</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.1</SNumber>
</UpperBound>
</Tolerance>
</TolerancedNumberMatrix>
Validation:
This type is validated using the XML Schema file.
The Schematron schema file checks that <NumberMatrix> and <ToleranceMatrix> have the same dimension.
Attention
See Number Matrices, Tolerance Matrices, and Tolerances for details about <NumberMatrix>, <ToleranceMatrix>, and <Tolerance> element validation.
Unit Matrices¶
Formal definition (auto-generated documentation based on XSD file).
A unit matrix consists of one or more rows of Units.
Example:
<UnitMatrix>
<UnitMatrixRow>
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">metre</mml:csymbol>
</mml:math>
</Unit>
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">ampere</mml:csymbol>
</mml:math>
</Unit>
</UnitMatrixRow>
<UnitMatrixRow>
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">second</mml:csymbol>
</mml:math>
</Unit>
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">volt</mml:csymbol>
</mml:math>
</Unit>
</UnitMatrixRow>
<UnitMatrixRow>
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">gram</mml:csymbol>
</mml:math>
</Unit>
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">farad</mml:csymbol>
</mml:math>
</Unit>
</UnitMatrixRow>
</UnitMatrix>
Validation:
This type is validated using the XML Schema file.
Attention
See Units for details about <Unit> element validation.
Quantity Matrices¶
Formal definition (auto-generated documentation based on XSD file).
Quantity matrices comprise a number matrix (or sparse number matrix) and a unit matrix (or sparse unit matrix). If all quantities have the same unit, a single unit may be used instead of a matrix.
Example:
<QuantityMatrix>
<NumberMatrix>
<NumberMatrixRow>
<SNumber>1.0</SNumber>
<SNumber>2.0</SNumber>
</NumberMatrixRow>
<NumberMatrixRow>
<SNumber>1.5</SNumber>
<SNumber>3.0</SNumber>
</NumberMatrixRow>
<NumberMatrixRow>
<SNumber>2.0</SNumber>
<SNumber>4.0</SNumber>
</NumberMatrixRow>
</NumberMatrix>
<UnitMatrix>
<UnitMatrixRow>
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">metre</mml:csymbol>
</mml:math>
</Unit>
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">ampere</mml:csymbol>
</mml:math>
</Unit>
</UnitMatrixRow>
<UnitMatrixRow>
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">second</mml:csymbol>
</mml:math>
</Unit>
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">volt</mml:csymbol>
</mml:math>
</Unit>
</UnitMatrixRow>
<UnitMatrixRow>
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">gram</mml:csymbol>
</mml:math>
</Unit>
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">farad</mml:csymbol>
</mml:math>
</Unit>
</UnitMatrixRow>
</UnitMatrix>
</QuantityMatrix>
Example:
<QuantityMatrix>
<NumberMatrix>
<NumberMatrixRow>
<SNumber>1.0</SNumber>
<SNumber>2.0</SNumber>
</NumberMatrixRow>
<NumberMatrixRow>
<SNumber>1.5</SNumber>
<SNumber>3.0</SNumber>
</NumberMatrixRow>
<NumberMatrixRow>
<SNumber>2.0</SNumber>
<SNumber>4.0</SNumber>
</NumberMatrixRow>
</NumberMatrix>
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">metre</mml:csymbol>
</mml:math>
</Unit>
</QuantityMatrix>
Validation:
This type is validated using the XML Schema file.
The Schematron schema file checks that <NumberMatrix> and <UnitMatrix> have the same dimension.
Attention
See Number Matrices, Unit Matrices, and Units for details about <NumberMatrix>, <UnitMatrix>, and <Unit> element validation.
Toleranced Quantity Matrices¶
Formal definition (auto-generated documentation based on XSD file).
Matrices of toleranced quantities comprise a number matrix (or sparse number matrix), a tolerance matrix (or sparse tolerance matrix), and a unit matrix (or sparse unit matrix). If all quantities have the same tolerance/unit, a single tolerance/unit may be used instead of a matrix.
Example:
<TolerancedQuantityMatrix>
<NumberMatrix>
<NumberMatrixRow>
<SNumber>1.0</SNumber>
<SNumber>2.0</SNumber>
</NumberMatrixRow>
<NumberMatrixRow>
<SNumber>1.5</SNumber>
<SNumber>3.0</SNumber>
</NumberMatrixRow>
<NumberMatrixRow>
<SNumber>2.0</SNumber>
<SNumber>4.0</SNumber>
</NumberMatrixRow>
</NumberMatrix>
<ToleranceMatrix>
<ToleranceMatrixRow>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.1</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.1</SNumber>
</UpperBound>
</Tolerance>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.2</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.2</SNumber>
</UpperBound>
</Tolerance>
</ToleranceMatrixRow>
<ToleranceMatrixRow>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.15</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.15</SNumber>
</UpperBound>
</Tolerance>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.3</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.3</SNumber>
</UpperBound>
</Tolerance>
</ToleranceMatrixRow>
<ToleranceMatrixRow>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.2</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.2</SNumber>
</UpperBound>
</Tolerance>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.4</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.4</SNumber>
</UpperBound>
</Tolerance>
</ToleranceMatrixRow>
</ToleranceMatrix>
<UnitMatrix>
<UnitMatrixRow>
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">metre</mml:csymbol>
</mml:math>
</Unit>
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">ampere</mml:csymbol>
</mml:math>
</Unit>
</UnitMatrixRow>
<UnitMatrixRow>
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">second</mml:csymbol>
</mml:math>
</Unit>
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">volt</mml:csymbol>
</mml:math>
</Unit>
</UnitMatrixRow>
<UnitMatrixRow>
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">gram</mml:csymbol>
</mml:math>
</Unit>
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">farad</mml:csymbol>
</mml:math>
</Unit>
</UnitMatrixRow>
</UnitMatrix>
</TolerancedQuantityMatrix>
Example:
<TolerancedQuantityMatrix>
<NumberMatrix>
<NumberMatrixRow>
<SNumber>1.0</SNumber>
<SNumber>2.0</SNumber>
</NumberMatrixRow>
<NumberMatrixRow>
<SNumber>1.5</SNumber>
<SNumber>3.0</SNumber>
</NumberMatrixRow>
<NumberMatrixRow>
<SNumber>2.0</SNumber>
<SNumber>4.0</SNumber>
</NumberMatrixRow>
</NumberMatrix>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.1</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.1</SNumber>
</UpperBound>
</Tolerance>
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">metre</mml:csymbol>
</mml:math>
</Unit>
</TolerancedQuantityMatrix>
Validation:
This type is validated using the XML Schema file.
The Schematron schema file checks that <NumberMatrix>, <ToleranceMatrix>, and <UnitMatrix> have the same dimension.
Attention
See Number Matrices, Tolerance Matrices, Unit Matrices, Tolerances, and Units for details about <NumberMatrix>, <ToleranceMatrix>, <UnitMatrix>, <Tolerance> and <Unit> element validation.
Sparse Matrices¶
Just like normal matrices, sparse matrices are 2-dimensional arrays of elements. In a sparse matrix, most elements have the same value. Therefore, for each sparse matrix, a default value is specified, as well as all elements that are not equal to this default value.
All types of sparse matrices share the same structure:
- Attributes:
- RowCount [xsd:positiveInteger] – number of rows in the sparse matrix
- ColumnCount [xsd:positiveInteger] – number of columns in the sparse matrix
- DefaultElement – default element
- element (by value or by reference)
- Elements
- Element (1..∞):
- Attributes:
- RowIndex [xsd:positiveInteger] – one-based row index of the element
- ColumnIndex [xsd:positiveInteger] – one-based column index of the element
- element (by value or by reference)
Sparse String Matrices¶
Formal definition (auto-generated documentation based on XSD file).
A sparse string matrix consists of one or more rows of Strings.
Example:
<StringSparseMatrix RowCount="3" ColumnCount="2">
<DefaultElement>
<String>Vdd</String>
</DefaultElement>
<Elements>
<Element RowIndex="3" ColumnIndex="1">
<String>Vss</String>
</Element>
</Elements>
</StringSparseMatrix>
Validation:
This type is validated using the XML Schema file.
Sparse Number Matrices¶
Formal definition (auto-generated documentation based on XSD file).
A sparse number matrix consists of one or more rows of Numbers.
Each row may contain both, <SNumber> and <MNumber> elements.
Example:
<NumberSparseMatrix RowCount="3" ColumnCount="2">
<DefaultElement>
<SNumber>1.0</SNumber>
</DefaultElement>
<Elements>
<Element RowIndex="3" ColumnIndex="1">
<SNumber>2.0</SNumber>
</Element>
</Elements>
</NumberSparseMatrix>
Validation:
This type is validated using the XML Schema file.
Attention
See Simple Numbers and MathML Numbers for details about <SNumber> and <MNumber> element validation.
Sparse Tolerance Matrices¶
Formal definition (auto-generated documentation based on XSD file).
A sparse tolerance matrix consists of one or more rows of Tolerances.
Example:
<ToleranceSparseMatrix RowCount="3" ColumnCount="2">
<DefaultElement>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.1</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.1</SNumber>
</UpperBound>
</Tolerance>
</DefaultElement>
<Elements>
<Element RowIndex="3" ColumnIndex="1">
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.2</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.2</SNumber>
</UpperBound>
</Tolerance>
</Element>
</Elements>
</ToleranceSparseMatrix>
Validation:
This type is validated using the XML Schema file.
Attention
See Tolerances for details about <Tolerance> element validation.
Sparse Toleranced Number Matrices¶
Formal definition (auto-generated documentation based on XSD file).
A sparse toleranced number matrix consists of one or more rows of Toleranced Numbers.
Example:
<TolerancedNumberSparseMatrix RowCount="3" ColumnCount="2">
<DefaultElement>
<TolerancedNumber>
<SNumber>1.0</SNumber>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.1</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.1</SNumber>
</UpperBound>
</Tolerance>
</TolerancedNumber>
</DefaultElement>
<Elements>
<Element RowIndex="3" ColumnIndex="1">
<TolerancedNumber>
<SNumber>2.0</SNumber>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.2</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.2</SNumber>
</UpperBound>
</Tolerance>
</TolerancedNumber>
</Element>
</Elements>
</TolerancedNumberSparseMatrix>
Validation:
This type is validated using the XML Schema file.
Attention
See Toleranced Numbers for details about <TolerancedNumber> element validation.
Sparse Unit Matrices¶
Formal definition (auto-generated documentation based on XSD file).
A sparse unit matrix consists of one or more rows of Units.
Example:
<UnitSparseMatrix RowCount="3" ColumnCount="2">
<DefaultElement>
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">metre</mml:csymbol>
</mml:math>
</Unit>
</DefaultElement>
<Elements>
<Element RowIndex="3" ColumnIndex="1">
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">gram</mml:csymbol>
</mml:math>
</Unit>
</Element>
</Elements>
</UnitSparseMatrix>
Validation:
This type is validated using the XML Schema file.
Attention
See Units for details about <Unit> element validation.
Sparse Quantity Matrices¶
Formal definition (auto-generated documentation based on XSD file).
A sparse quantity matrix consists of one or more rows of Quantities.
Example:
<QuantitySparseMatrix RowCount="3" ColumnCount="2">
<DefaultElement>
<Quantity>
<SNumber>1.0</SNumber>
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">metre</mml:csymbol>
</mml:math>
</Unit>
</Quantity>
</DefaultElement>
<Elements>
<Element RowIndex="3" ColumnIndex="1">
<Quantity>
<SNumber>2.0</SNumber>
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">gram</mml:csymbol>
</mml:math>
</Unit>
</Quantity>
</Element>
</Elements>
</QuantitySparseMatrix>
Validation:
This type is validated using the XML Schema file.
Attention
See Quantities for details about <Quantity> element validation.
Sparse Toleranced Quantity Matrices¶
Formal definition (auto-generated documentation based on XSD file).
A sparse toleranced quantity matrix consists of one or more rows of Toleranced Quantities.
Example:
<TolerancedQuantitySparseMatrix RowCount="3" ColumnCount="2">
<DefaultElement>
<TolerancedQuantity>
<SNumber>1.0</SNumber>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.1</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.1</SNumber>
</UpperBound>
</Tolerance>
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">metre</mml:csymbol>
</mml:math>
</Unit>
</TolerancedQuantity>
</DefaultElement>
<Elements>
<Element RowIndex="3" ColumnIndex="1">
<TolerancedQuantity>
<SNumber>2.0</SNumber>
<Tolerance>
<LowerBound BoundType="absolute">
<SNumber>0.2</SNumber>
</LowerBound>
<UpperBound BoundType="absolute">
<SNumber>0.2</SNumber>
</UpperBound>
</Tolerance>
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">gram</mml:csymbol>
</mml:math>
</Unit>
</TolerancedQuantity>
</Element>
</Elements>
</TolerancedQuantitySparseMatrix>
Validation:
This type is validated using the XML Schema file.
Attention
See Toleranced Quantities for details about <TolerancedQuantity> element validation.
Formula Templates¶
Formal definition (auto-generated documentation based on XSD file).
Formula templates are parameterized mathematical expressions, i.e. their value depends not only on their arguments, but also on additional parameters. However, they do not specify the units of the formula’s value or its arguments. Therefore, they represent a purely symbolic mathematical expression, without indicating its domain or codomain. They are described by a symbol, a list of arguments, a list of parameters, and their mathematical expression. Only the symbol must be specified for all arguments.
- Attributes:
- Symbol [xsd:string] – Formula symbol
- TeX [xsd:string] (optional) – LaTeX formula symbol
- Arguments (optional):
- Argument (1..∞):
- Attributes:
- Symbol [xsd:string] – argument symbol
- TeX [xsd:string] (optional) – LaTeX argument symbol
- Parameters (optional):
- Parameter (1..∞):
- Attributes:
- Symbol [xsd:string] – parameter symbol
- TeX [xsd:string] (optional) – LaTeX parameter symbol
- math – Strict Content MathML description of the formula that may use previously defined arguments and parameters.
Example:
Expression: \(U(t)\)
Parameters: \(U_0\), \(s\)
<FormulaTemplate Symbol="U">
<Arguments>
<Argument Symbol="t"/>
</Arguments>
<Parameters>
<Parameter Symbol="U0" TeX="U_0"/>
<Parameter Symbol="s"/>
</Parameters>
<mml:math>
<mml:apply>
<mml:csymbol cd="arith1">plus</mml:csymbol>
<mml:ci>U0</mml:ci>
<mml:apply>
<mml:csymbol cd="arith1">times</mml:csymbol>
<mml:ci>s</mml:ci>
<mml:ci>t</mml:ci>
</mml:apply>
</mml:apply>
</mml:math>
</FormulaTemplate>
Validation:
This type is validated using the XML Schema file.
Note
Strict Content MathML formula descriptions in <mml:math> elements are validated using the official RelaxNG schema via mpfo.nvdl.
Attention
It is not validated whether parameter symbols are unique in a formula template.
Formulas¶
Formal definition (auto-generated documentation based on XSD file).
Formulas describe mathematical expressions whose value depends only on their arguments, i.e. that have no additional parameters. However, they do not specify the units of the formula’s value or its arguments. Therefore, they represent a purely symbolic mathematical expression, without indicating its domain or codomain. They are described by a formula template (that may depend on parameters) and a list of values for all template parameters. Parameter values are defined as quantities that include the value’s magnitude (as numerical value) and unit.
FormulaTemplate – Formula template on which the formula is based
- ParameterValues (optional):
- ParameterValue (1..∞):
- Attributes:
- Symbol [xsd:string] – parameter symbol; used to identify the associated parameter of the formula template
*Quantity* – Quantity value of the parameter (including the value’s magnitude and unit); can be a quantity, quantity interval, quantity vector, sparse quantity vector, quantity matrix, sparse quantity matrix, toleranced quantity, toleranced quantity interval, toleranced quantity vector, sparse toleranced quantity vector, toleranced quantity matrix, sparse toleranced quantity matrix or function.
Attention
When using a function as a quantity value, its argument list must be identical to the argument list of the formula template. This is currently not validated.
Example:
Expression: \(U(t)\)
Parameters: \(U_0 = 3.3\,\text{V}\), \(s = 2\,\frac{\text{V}}{\text{s}}\)
<Formula>
<FormulaTemplate Symbol="U">
<Arguments>
<Argument Symbol="t"/>
</Arguments>
<Parameters>
<Parameter Symbol="U0" TeX="U_0"/>
<Parameter Symbol="s"/>
</Parameters>
<mml:math>
<mml:apply>
<mml:csymbol cd="arith1">plus</mml:csymbol>
<mml:ci>U0</mml:ci>
<mml:apply>
<mml:csymbol cd="arith1">times</mml:csymbol>
<mml:ci>s</mml:ci>
<mml:ci>t</mml:ci>
</mml:apply>
</mml:apply>
</mml:math>
</FormulaTemplate>
<ParameterValues>
<ParameterValue Symbol="U0">
<Quantity>
<SNumber>3.3</SNumber>
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">volt</mml:csymbol>
</mml:math>
</Unit>
</Quantity>
</ParameterValue>
<ParameterValue Symbol="s">
<Quantity>
<SNumber>2.0</SNumber>
<Unit>
<mml:math>
<mml:apply>
<mml:csymbol cd="arith1">divide</mml:csymbol>
<mml:csymbol cd="SI_NamedDerivedUnits1">volt</mml:csymbol>
<mml:csymbol cd="SI_BaseUnits1">second</mml:csymbol>
</mml:apply>
</mml:math>
</Unit>
</Quantity>
</ParameterValue>
</ParameterValues>
</Formula>
Validation:
This type is validated using the XML Schema file.
Attention
- See Formula Templates for details about validation of
<FormulaTemplate>elements. - See Quantities, Quantity Intervals, Quantity Vectors, Sparse Quantity Vectors, Quantity Matrices, Sparse Quantity Matrices, Toleranced Quantities, Toleranced Quantity Intervals, Toleranced Quantity Vectors, Sparse Toleranced Quantity Vectors, Toleranced Quantity Matrices, Sparse Toleranced Quantity Matrices and Functions for details about validation of
<ParameterValue>elements.
Attention
- It is not validated whether parameters with the specified symbols exist in the formula template.
- It is not validated whether values for all parameters of the formula template have been specified.
Functions¶
Functions map each element of a set \(X\) to a unique element of a set \(Y\). The first set is the functions domain and the second set is its codomain.
Currently, we support two types of functions: symbolic functions and table functions. Symbolic functions are defined in terms of a mathematical expression. Table functions are specified by their value table that includes all points for which the function is defined. Therefore, they are useful for the definition of, e.g., histograms.
For both types of functions, the domain and codomain are implicitly defined by the given units of the function’s value and its arguments.
Symbolic Function Templates¶
Formal definition (auto-generated documentation based on XSD file).
Symbolic function templates are parameterized mathematical functions, i.e. their value depends not only on their arguments, but also on additional parameters. They are described by a symbol, a unit, a list of arguments, a list of parameters, and their mathematical expression. For all arguments and parameters, the corresponding unit must be specified.
- Attributes:
- Symbol [xsd:string] – Function symbol
- TeX [xsd:string] (optional) – LaTeX function symbol
- Unit – Unit of the resulting quantity; can be a unit, unit vector, sparse unit vector, unit matrix, or sparse unit matrix
- Arguments (optional):
- ArgumentWithUnit (1..∞):
- Attributes:
- Symbol [xsd:string] – argument symbol
- TeX [xsd:string] (optional) – LaTeX argument symbol
- Unit – Unit of the argument; can be a unit, unit vector, sparse unit vector, unit matrix, or sparse unit matrix
- Parameters (optional):
- ParameterWithUnit (1..∞):
- Attributes:
- Symbol [xsd:string] – parameter symbol
- TeX [xsd:string] (optional) – LaTeX parameter symbol
- Unit – Unit of the parameter; can be a unit, unit vector, sparse unit vector, unit matrix, or sparse unit matrix
- math – Strict Content MathML description of the function that may use previously defined arguments and parameters.
Example 1:
Function: \(U(t)\) with \(\{U\}\) in V, \(\{t\}\) in s
Parameters: \(U_0\) in V

<SymbolicFunctionTemplate Symbol="U">
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">volt</mml:csymbol>
</mml:math>
</Unit>
<Arguments>
<ArgumentWithUnit Symbol="t">
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">second</mml:csymbol>
</mml:math>
</Unit>
</ArgumentWithUnit>
</Arguments>
<Parameters>
<ParameterWithUnit Symbol="U0" TeX="U_0">
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">volt</mml:csymbol>
</mml:math>
</Unit>
</ParameterWithUnit>
</Parameters>
<mml:math>
<mml:ci>U0</mml:ci>
</mml:math>
</SymbolicFunctionTemplate>
Example 2:
Function: \(U(t)\) with \(\{U\}\) in V, \(\{t\}\) in s
Parameters: \(U_0\) in V, \(f\) in Hz
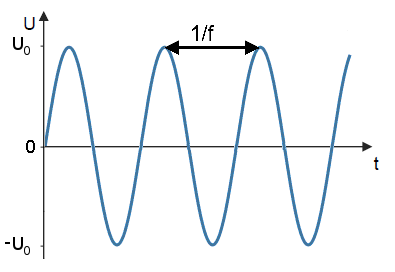
<SymbolicFunctionTemplate Symbol="U">
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">volt</mml:csymbol>
</mml:math>
</Unit>
<Arguments>
<ArgumentWithUnit Symbol="t">
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">second</mml:csymbol>
</mml:math>
</Unit>
</ArgumentWithUnit>
</Arguments>
<Parameters>
<ParameterWithUnit Symbol="U0" TeX="U_0">
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">volt</mml:csymbol>
</mml:math>
</Unit>
</ParameterWithUnit>
<ParameterWithUnit Symbol="f">
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">hertz</mml:csymbol>
</mml:math>
</Unit>
</ParameterWithUnit>
</Parameters>
<mml:math>
<mml:apply>
<mml:csymbol cd="arith1">times</mml:csymbol>
<mml:ci>U0</mml:ci>
<mml:apply>
<mml:csymbol cd="transc1">sin</mml:csymbol>
<mml:apply>
<mml:csymbol cd="arith1">times</mml:csymbol>
<mml:cn type="integer">2</mml:cn>
<mml:csymbol cd="nums1">pi</mml:csymbol>
<mml:ci>f</mml:ci>
</mml:apply>
</mml:apply>
</mml:apply>
</mml:math>
</SymbolicFunctionTemplate>
Example 3: Test pulse E-01 (long-term overvoltage) from LV124 / VW80000
Function: \(U(t)\) with \(\{U\}\) in V, \(\{t\}\) in s
Parameters: \(U_\text{max}\) in V, \(U_\text{min}\) in V, \(t_\text{r}\) in s, \(t_\text{f}\) in s, \(t_1\) in s
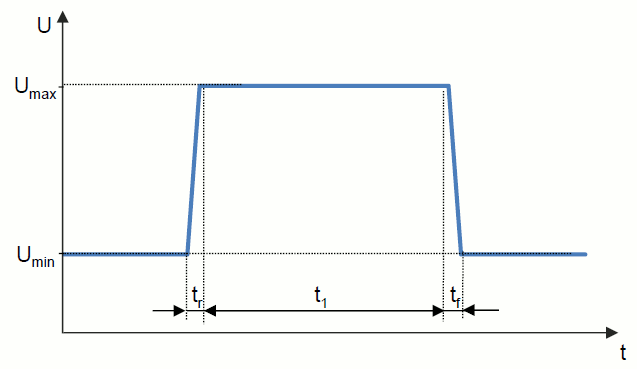
<SymbolicFunctionTemplate Symbol="U">
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">volt</mml:csymbol>
</mml:math>
</Unit>
<Arguments>
<ArgumentWithUnit Symbol="t">
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">second</mml:csymbol>
</mml:math>
</Unit>
</ArgumentWithUnit>
</Arguments>
<Parameters>
<ParameterWithUnit Symbol="Umax" TeX="U_\text{max}">
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">volt</mml:csymbol>
</mml:math>
</Unit>
</ParameterWithUnit>
<ParameterWithUnit Symbol="Umin" TeX="U_\text{min}">
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">volt</mml:csymbol>
</mml:math>
</Unit>
</ParameterWithUnit>
<ParameterWithUnit Symbol="tr" TeX="t_\text{r}">
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">seconds</mml:csymbol>
</mml:math>
</Unit>
</ParameterWithUnit>
<ParameterWithUnit Symbol="tf" TeX="t_\text{f}">
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">seconds</mml:csymbol>
</mml:math>
</Unit>
</ParameterWithUnit>
<ParameterWithUnit Symbol="t1" TeX="t_1">
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">seconds</mml:csymbol>
</mml:math>
</Unit>
</ParameterWithUnit>
</Parameters>
<mml:math>
<mml:apply>
<mml:csymbol cd="piece1">piecewise</mml:csymbol>
<mml:apply>
<mml:csymbol cd="piece1">piece</mml:csymbol>
<!-- ((Umax - Umin) / tr) * t + Umin -->
<mml:apply>
<mml:csymbol cd="arith1">plus</mml:csymbol>
<mml:apply>
<mml:csymbol cd="arith1">times</mml:csymbol>
<mml:apply>
<mml:csymbol cd="arith1">divide</mml:csymbol>
<mml:apply>
<mml:csymbol cd="arith1">minus</mml:csymbol>
<mml:ci>Umax</mml:ci>
<mml:ci>Umin</mml:ci>
</mml:apply>
<mml:ci>tr</mml:ci>
</mml:apply>
<mml:ci>t</mml:ci>
</mml:apply>
<mml:ci>Umin</mml:ci>
</mml:apply>
<!-- 0 <= t <= tr -->
<mml:apply>
<mml:csymbol cd="logic1">and</mml:csymbol>
<mml:apply>
<mml:csymbol cd="relation1">geq</mml:csymbol>
<mml:ci>t</mml:ci>
<mml:cn type="real">0</mml:cn>
</mml:apply>
<mml:apply>
<mml:csymbol cd="relation1">leq</mml:csymbol>
<mml:ci>t</mml:ci>
<mml:ci>tr</mml:ci>
</mml:apply>
</mml:apply>
</mml:apply>
<mml:apply>
<mml:csymbol cd="piece1">piece</mml:csymbol>
<!-- Umax -->
<mml:ci>Umax</mml:ci>
<!-- tr < t <= tr+t1 -->
<mml:apply>
<mml:csymbol cd="logic1">and</mml:csymbol>
<mml:apply>
<mml:csymbol cd="relation1">gt</mml:csymbol>
<mml:ci>t</mml:ci>
<mml:ci>tr</mml:ci>
</mml:apply>
<mml:apply>
<mml:csymbol cd="relation1">leq</mml:csymbol>
<mml:ci>t</mml:ci>
<mml:apply>
<mml:csymbol cd="arith1">plus</mml:csymbol>
<mml:ci>tr</mml:ci>
<mml:ci>t1</mml:ci>
</mml:apply>
</mml:apply>
</mml:apply>
</mml:apply>
<mml:apply>
<mml:csymbol cd="piece1">piece</mml:csymbol>
<!-- ((Umin - Umax) / tf) * (t - tr - t1) + Umax-->
<mml:apply>
<mml:csymbol cd="arith1">plus</mml:csymbol>
<mml:apply>
<mml:csymbol cd="arith1">times</mml:csymbol>
<mml:apply>
<mml:csymbol cd="arith1">divide</mml:csymbol>
<mml:apply>
<mml:csymbol cd="arith1">minus</mml:csymbol>
<mml:ci>Umin</mml:ci>
<mml:ci>Umax</mml:ci>
</mml:apply>
<mml:ci>tf</mml:ci>
</mml:apply>
<mml:apply>
<mml:csymbol cd="arith1">minus</mml:csymbol>
<mml:ci>t</mml:ci>
<mml:ci>tr</mml:ci>
<mml:ci>t1</mml:ci>
</mml:apply>
</mml:apply>
<mml:ci>Umax</mml:ci>
</mml:apply>
<!-- tr+t1 < t <= tr+t1+tf -->
<mml:apply>
<mml:csymbol cd="logic1">and</mml:csymbol>
<mml:apply>
<mml:csymbol cd="relation1">gt</mml:csymbol>
<mml:ci>t</mml:ci>
<mml:apply>
<mml:csymbol cd="arith1">plus</mml:csymbol>
<mml:ci>tr</mml:ci>
<mml:ci>t1</mml:ci>
</mml:apply>
</mml:apply>
<mml:apply>
<mml:csymbol cd="relation1">leq</mml:csymbol>
<mml:ci>t</mml:ci>
<mml:apply>
<mml:csymbol cd="arith1">plus</mml:csymbol>
<mml:ci>tr</mml:ci>
<mml:ci>t1</mml:ci>
<mml:ci>tf</mml:ci>
</mml:apply>
</mml:apply>
</mml:apply>
</mml:apply>
</mml:apply>
</mml:math>
</SymbolicFunctionTemplate>
Example 4: Test pule E-06 (superimposed AC voltage) from LV124 / VW80000
Function: \(U(t)\) with \(\{U\}\) in V, \(\{t\}\) in s
Parameters: \(U_\text{max}\) in V, \(U_\text{pp}\) in V, \(f_\text{min}\) in Hz, \(f_\text{max}\) in Hz, \(t_1\) in s
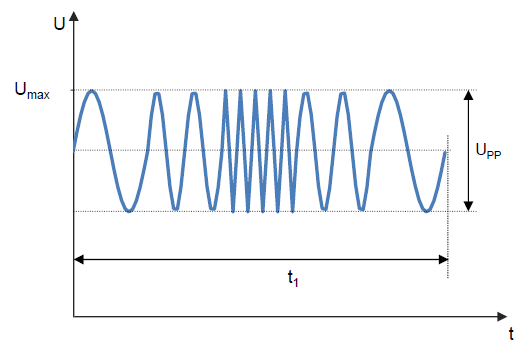
<SymbolicFunctionTemplate Symbol="U">
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">volt</mml:csymbol>
</mml:math>
</Unit>
<Arguments>
<ArgumentWithUnit Symbol="t">
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">second</mml:csymbol>
</mml:math>
</Unit>
</ArgumentWithUnit>
</Arguments>
<Parameters>
<ParameterWithUnit Symbol="Umax" TeX="U_\text{max}">
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">volt</mml:csymbol>
</mml:math>
</Unit>
</ParameterWithUnit>
<ParameterWithUnit Symbol="Upp" TeX="U_\text{pp}">
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">volt</mml:csymbol>
</mml:math>
</Unit>
</ParameterWithUnit>
<ParameterWithUnit Symbol="fmin" TeX="f_\text{min}">
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">hertz</mml:csymbol>
</mml:math>
</Unit>
</ParameterWithUnit>
<ParameterWithUnit Symbol="fmax" TeX="f_\text{max}">
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">hertz</mml:csymbol>
</mml:math>
</Unit>
</ParameterWithUnit>
<ParameterWithUnit Symbol="t1" TeX="t_1">
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">seconds</mml:csymbol>
</mml:math>
</Unit>
</ParameterWithUnit>
</Parameters>
<mml:math>
<mml:apply>
<mml:csymbol cd="piece1">piecewise</mml:csymbol>
<mml:apply>
<mml:csymbol cd="piece1">piece</mml:csymbol>
<mml:apply>
<mml:csymbol cd="arith1">plus</mml:csymbol>
<mml:apply>
<mml:csymbol cd="arith1">minus</mml:csymbol>
<mml:ci>Umax</mml:ci>
<mml:apply>
<mml:csymbol cd="arith1">divide</mml:csymbol>
<mml:ci>Upp</mml:ci>
<mml:cn type="integer">2</mml:cn>
</mml:apply>
</mml:apply>
<mml:apply>
<mml:csymbol cd="arith1">times</mml:csymbol>
<mml:apply>
<mml:csymbol cd="arith1">divide</mml:csymbol>
<mml:ci>Upp</mml:ci>
<mml:cn type="integer">2</mml:cn>
</mml:apply>
<mml:apply>
<mml:csymbol cd="transc1">sin</mml:csymbol>
<mml:apply>
<mml:csymbol cd="arith1">times</mml:csymbol>
<mml:cn type="integer">2</mml:cn>
<mml:csymbol cd="nums1">pi</mml:csymbol>
<mml:apply>
<mml:csymbol cd="transc1">exp</mml:csymbol>
<mml:apply>
<mml:csymbol cd="arith1">plus</mml:csymbol>
<mml:apply>
<mml:csymbol cd="arith1">times</mml:csymbol>
<mml:apply>
<mml:csymbol cd="transc1">ln</mml:csymbol>
<mml:apply>
<mml:csymbol cd="arith1">divide</mml:csymbol>
<mml:ci>fmax</mml:ci>
<mml:ci>fmin</mml:ci>
</mml:apply>
</mml:apply>
<mml:apply>
<mml:csymbol cd="arith1">divide</mml:csymbol>
<mml:cn type="integer">2</mml:cn>
<mml:ci>t1</mml:ci>
</mml:apply>
<mml:ci>t</mml:ci>
</mml:apply>
<mml:apply>
<mml:csymbol cd="transc1">ln</mml:csymbol>
<mml:ci>fmin</mml:ci>
</mml:apply>
</mml:apply><!-- plus -->
</mml:apply><!-- exp -->
</mml:apply><!-- times -->
</mml:apply><!-- sin -->
</mml:apply><!-- times -->
</mml:apply><!-- plus -->
<mml:apply>
<mml:csymbol cd="logic1">and</mml:csymbol>
<mml:apply>
<mml:csymbol cd="relation1">geq</mml:csymbol>
<mml:ci>t</mml:ci>
<mml:cn type="real">0</mml:cn>
</mml:apply>
<mml:apply>
<mml:csymbol cd="relation1">leq</mml:csymbol>
<mml:ci>t</mml:ci>
<mml:apply>
<mml:csymbol cd="arith1">divide</mml:csymbol>
<mml:ci>t1</mml:ci>
<mml:cn type="integer">2</mml:cn>
</mml:apply>
</mml:apply>
</mml:apply>
</mml:apply>
<mml:apply>
<mml:csymbol cd="piece1">piece</mml:csymbol>
<mml:apply>
<mml:csymbol cd="arith1">plus</mml:csymbol>
<mml:apply>
<mml:csymbol cd="arith1">minus</mml:csymbol>
<mml:ci>Umax</mml:ci>
<mml:apply>
<mml:csymbol cd="arith1">divide</mml:csymbol>
<mml:ci>Upp</mml:ci>
<mml:cn type="integer">2</mml:cn>
</mml:apply>
</mml:apply>
<mml:apply>
<mml:csymbol cd="arith1">times</mml:csymbol>
<mml:apply>
<mml:csymbol cd="arith1">divide</mml:csymbol>
<mml:ci>Upp</mml:ci>
<mml:cn type="integer">2</mml:cn>
</mml:apply>
<mml:apply>
<mml:csymbol cd="transc1">sin</mml:csymbol>
<mml:apply>
<mml:csymbol cd="arith1">times</mml:csymbol>
<mml:apply>
<mml:csymbol cd="arith1">unary_minus</mml:csymbol>
<mml:cn type="integer">2</mml:cn>
</mml:apply>
<mml:csymbol cd="nums1">pi</mml:csymbol>
<mml:apply>
<mml:csymbol cd="transc1">exp</mml:csymbol>
<mml:apply>
<mml:csymbol cd="arith1">plus</mml:csymbol>
<mml:apply>
<mml:csymbol cd="arith1">times</mml:csymbol>
<mml:apply>
<mml:csymbol cd="transc1">ln</mml:csymbol>
<mml:apply>
<mml:csymbol cd="arith1">divide</mml:csymbol>
<mml:ci>fmin</mml:ci>
<mml:ci>fmax</mml:ci>
</mml:apply>
</mml:apply>
<mml:apply>
<mml:csymbol cd="arith1">divide</mml:csymbol>
<mml:cn type="integer">2</mml:cn>
<mml:ci>t1</mml:ci>
</mml:apply>
<mml:apply>
<mml:csymbol cd="arith1">minus</mml:csymbol>
<mml:ci>t</mml:ci>
<mml:apply>
<mml:csymbol cd="arith1">divide</mml:csymbol>
<mml:ci>t1</mml:ci>
<mml:cn type="integer">2</mml:cn>
</mml:apply>
</mml:apply>
</mml:apply>
<mml:apply>
<mml:csymbol cd="transc1">ln</mml:csymbol>
<mml:ci>fmax</mml:ci>
</mml:apply>
</mml:apply><!-- plus -->
</mml:apply><!-- exp -->
</mml:apply><!-- times -->
</mml:apply><!-- sin -->
</mml:apply><!-- times -->
</mml:apply><!-- plus -->
<mml:apply>
<mml:csymbol cd="logic1">and</mml:csymbol>
<mml:apply>
<mml:csymbol cd="relation1">gt</mml:csymbol>
<mml:ci>t</mml:ci>
<mml:ci>t</mml:ci>
<mml:apply>
<mml:csymbol cd="arith1">divide</mml:csymbol>
<mml:ci>t1</mml:ci>
<mml:cn type="integer">2</mml:cn>
</mml:apply>
</mml:apply>
<mml:apply>
<mml:csymbol cd="relation1">leq</mml:csymbol>
<mml:ci>t</mml:ci>
<mml:ci>t1</mml:ci>
</mml:apply>
</mml:apply>
</mml:apply>
</mml:apply>
</mml:math>
</SymbolicFunctionTemplate>
Example 5: Test pulse E-07 (gradual lowering and raising of the supply voltage) from LV124 / VW80000
Function: \(U(t)\) with \(\{U\}\) in V, \(\{t\}\) in min
Parameters: \(U_\text{start}\) in V, \(m\) in V/min, \(U_1\) in V, \(t_1\) in min, \(U_\text{min}\) in V, \(U_2\) in V, \(t_2\) in min, \(U_\text{end}\) in V
<SymbolicFunctionTemplate Symbol="U">
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">volt</mml:csymbol>
</mml:math>
</Unit>
<Arguments>
<ArgumentWithUnit Symbol="t">
<Unit>
<mml:math>
<mml:csymbol cd="SIUsed_OffSystemUnits1">minute</mml:csymbol>
</mml:math>
</Unit>
</ArgumentWithUnit>
</Arguments>
<Parameters>
<ParameterWithUnit Symbol="Ustart" TeX="U_\text{start}">
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">volt</mml:csymbol>
</mml:math>
</Unit>
</ParameterWithUnit>
<ParameterWithUnit Symbol="m">
<Unit>
<mml:math>
<mml:apply>
<mml:csymbol cd="arith1">divide</mml:csymbol>
<mml:csymbol cd="SI_NamedDerivedUnits1">volt</mml:csymbol>
<mml:csymbol cd="SIUsed_OffSystemUnits1">minute</mml:csymbol>
</mml:apply>
</mml:math>
</Unit>
</ParameterWithUnit>
<ParameterWithUnit Symbol="U1" TeX="U_1">
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">volt</mml:csymbol>
</mml:math>
</Unit>
</ParameterWithUnit>
<ParameterWithUnit Symbol="t1" TeX="t_1">
<Unit>
<mml:math>
<mml:csymbol cd="SIUsed_OffSystemUnits1">minute</mml:csymbol>
</mml:math>
</Unit>
</ParameterWithUnit>
<ParameterWithUnit Symbol="Umin" TeX="U_\text{min}">
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">volt</mml:csymbol>
</mml:math>
</Unit>
</ParameterWithUnit>
<ParameterWithUnit Symbol="U2" TeX="U_2">
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">volt</mml:csymbol>
</mml:math>
</Unit>
</ParameterWithUnit>
<ParameterWithUnit Symbol="t2" TeX="t_2">
<Unit>
<mml:math>
<mml:csymbol cd="SIUsed_OffSystemUnits1">minute</mml:csymbol>
</mml:math>
</Unit>
</ParameterWithUnit>
<ParameterWithUnit Symbol="Uend" TeX="U_\text{end}">
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">volt</mml:csymbol>
</mml:math>
</Unit>
</ParameterWithUnit>
</Parameters>
<mml:math>
<mml:apply>
<mml:csymbol cd="piece1">piecewise</mml:csymbol>
<mml:apply>
<mml:csymbol cd="piece1">piece</mml:csymbol>
<mml:apply>
<mml:csymbol cd="arith1">plus</mml:csymbol>
<mml:apply>
<mml:csymbol cd="arith1">times</mml:csymbol>
<mml:apply>
<mml:csymbol cd="arith1">unary_minus</mml:csymbol>
<mml:ci>m</mml:ci>
</mml:apply>
<mml:ci>t</mml:ci>
</mml:apply>
<mml:ci>Ustart</mml:ci>
</mml:apply>
<mml:apply>
<mml:csymbol cd="logic1">and</mml:csymbol>
<mml:apply>
<mml:csymbol cd="relation1">geq</mml:csymbol>
<mml:ci>t</mml:ci>
<mml:cn type="real">0</mml:cn>
</mml:apply>
<mml:apply>
<mml:csymbol cd="relation1">leq</mml:csymbol>
<mml:ci>t</mml:ci>
<mml:apply id="i1end">
<mml:csymbol cd="arith1">divide</mml:csymbol>
<mml:apply>
<mml:csymbol cd="arith1">minus</mml:csymbol>
<mml:ci>Ustart</mml:ci>
<mml:ci>U1</mml:ci>
</mml:apply>
<mml:ci>m</mml:ci>
</mml:apply>
</mml:apply>
</mml:apply>
</mml:apply>
<mml:apply>
<mml:csymbol cd="piece1">piece</mml:csymbol>
<mml:ci>U1</mml:ci>
<mml:apply>
<mml:csymbol cd="logic1">and</mml:csymbol>
<mml:apply>
<mml:csymbol cd="relation1">gt</mml:csymbol>
<mml:ci>t</mml:ci>
<mml:share href="#i1end"/>
</mml:apply>
<mml:apply>
<mml:csymbol cd="relation1">leq</mml:csymbol>
<mml:ci>t</mml:ci>
<mml:apply id="i2end">
<mml:csymbol cd="arith1">plus</mml:csymbol>
<mml:share href="#i1end"/>
<mml:ci>t1</mml:ci>
</mml:apply>
</mml:apply>
</mml:apply>
</mml:apply>
<mml:apply>
<mml:csymbol cd="piece1">piece</mml:csymbol>
<mml:apply>
<mml:csymbol cd="arith1">plus</mml:csymbol>
<mml:apply>
<mml:csymbol cd="arith1">times</mml:csymbol>
<mml:apply>
<mml:csymbol cd="arith1">unary_minus</mml:csymbol>
<mml:ci>m</mml:ci>
</mml:apply>
<mml:apply>
<mml:csymbol cd="arith1">minus</mml:csymbol>
<mml:ci>t</mml:ci>
<mml:share href="#i2end"/>
</mml:apply>
</mml:apply>
<mml:ci>U1</mml:ci>
</mml:apply>
<mml:apply>
<mml:csymbol cd="logic1">and</mml:csymbol>
<mml:apply>
<mml:csymbol cd="relation1">gt</mml:csymbol>
<mml:ci>t</mml:ci>
<mml:share href="#i2end"/>
</mml:apply>
<mml:apply>
<mml:csymbol cd="relation1">leq</mml:csymbol>
<mml:ci>t</mml:ci>
<mml:apply id="i3end">
<mml:csymbol cd="arith1">plus</mml:csymbol>
<mml:share href="#i2end"/>
<mml:apply>
<mml:csymbol cd="arith1">divide</mml:csymbol>
<mml:apply>
<mml:csymbol cd="arith1">minus</mml:csymbol>
<mml:ci>U1</mml:ci>
<mml:ci>Umin</mml:ci>
</mml:apply>
<mml:ci>m</mml:ci>
</mml:apply>
</mml:apply>
</mml:apply>
</mml:apply>
</mml:apply>
<mml:apply>
<mml:csymbol cd="piece1">piece</mml:csymbol>
<mml:apply>
<mml:csymbol cd="arith1">plus</mml:csymbol>
<mml:apply>
<mml:csymbol cd="arith1">times</mml:csymbol>
<mml:ci>m</mml:ci>
<mml:apply>
<mml:csymbol cd="arith1">minus</mml:csymbol>
<mml:ci>t</mml:ci>
<mml:share href="#i3end"/>
</mml:apply>
</mml:apply>
<mml:ci>Umin</mml:ci>
</mml:apply>
<mml:apply>
<mml:csymbol cd="logic1">and</mml:csymbol>
<mml:apply>
<mml:csymbol cd="relation1">gt</mml:csymbol>
<mml:ci>t</mml:ci>
<mml:share href="#i3end"/>
</mml:apply>
<mml:apply>
<mml:csymbol cd="relation1">leq</mml:csymbol>
<mml:ci>t</mml:ci>
<mml:apply id="i4end">
<mml:csymbol cd="arith1">plus</mml:csymbol>
<mml:share href="#i3end"/>
<mml:apply>
<mml:csymbol cd="arith1">divide</mml:csymbol>
<mml:apply>
<mml:csymbol cd="arith1">minus</mml:csymbol>
<mml:ci>U2</mml:ci>
<mml:ci>Umin</mml:ci>
</mml:apply>
<mml:ci>m</mml:ci>
</mml:apply>
</mml:apply>
</mml:apply>
</mml:apply>
</mml:apply>
<mml:apply>
<mml:csymbol cd="piece1">piece</mml:csymbol>
<mml:ci>U2</mml:ci>
<mml:apply>
<mml:csymbol cd="logic1">and</mml:csymbol>
<mml:apply>
<mml:csymbol cd="relation1">gt</mml:csymbol>
<mml:ci>t</mml:ci>
<mml:share href="#i4end"/>
</mml:apply>
<mml:apply>
<mml:csymbol cd="relation1">leq</mml:csymbol>
<mml:ci>t</mml:ci>
<mml:apply id="i5end">
<mml:csymbol cd="arith1">plus</mml:csymbol>
<mml:share href="#i4end"/>
<mml:ci>t2</mml:ci>
</mml:apply>
</mml:apply>
</mml:apply>
</mml:apply>
<mml:apply>
<mml:csymbol cd="piece1">piece</mml:csymbol>
<mml:apply>
<mml:csymbol cd="arith1">plus</mml:csymbol>
<mml:apply>
<mml:csymbol cd="arith1">times</mml:csymbol>
<mml:ci>m</mml:ci>
<mml:apply>
<mml:csymbol cd="arith1">minus</mml:csymbol>
<mml:ci>t</mml:ci>
<mml:share href="#i5end"/>
</mml:apply>
</mml:apply>
<mml:ci>U2</mml:ci>
</mml:apply>
<mml:apply>
<mml:csymbol cd="logic1">and</mml:csymbol>
<mml:apply>
<mml:csymbol cd="relation1">gt</mml:csymbol>
<mml:ci>t</mml:ci>
<mml:share href="#i5end"/>
</mml:apply>
<mml:apply>
<mml:csymbol cd="relation1">leq</mml:csymbol>
<mml:ci>t</mml:ci>
<mml:apply id="i6end">
<mml:csymbol cd="arith1">plus</mml:csymbol>
<mml:share href="#i5end"/>
<mml:apply>
<mml:csymbol cd="arith1">divide</mml:csymbol>
<mml:apply>
<mml:csymbol cd="arith1">minus</mml:csymbol>
<mml:ci>Uend</mml:ci>
<mml:ci>U2</mml:ci>
</mml:apply>
<mml:ci>m</mml:ci>
</mml:apply>
</mml:apply>
</mml:apply>
</mml:apply>
</mml:apply>
</mml:apply>
</mml:math>
</SymbolicFunctionTemplate>
Validation:
This type is validated using the XML Schema file.
Note
Strict Content MathML function descriptions in <mml:math> elements are validated using the official RelaxNG schema via mpfo.nvdl.
Attention
See Units, Unit Vectors, Sparse Unit Vectors, Unit Matrices and Sparse Unit Matrices for details about validation of <Unit>, <UnitVector>, <UnitSparseVector>, <UnitMatrix> and <UnitSparseMatrix> elements.
Symbolic Functions¶
Formal definition (auto-generated documentation based on XSD file).
Symbolic functions describe symbolic mathematical functions whose value depends only on their arguments, i.e. that have no additional parameters. They are described by a symbolic function template (that may depend on parameters) and a list of values for all template parameters. The domain and codomain of a symbolic function are implicitly specified by the units of the function value and its arguments as defined by the template.
- SymbolicFunctionTemplate – Template on which the function is based
- ParameterValues (optional):
- ParameterValueMagnitude (1..∞):
- Attributes:
- Symbol [xsd:string] – parameter symbol; used to identify the associated parameter of the symbolic function template
- *Number* – Numeric value (magnitude) of the parameter (the symbolic function template defines the unit); can be a number, number interval, number interval vector, number vector, sparse number vector, number matrix, sparse number matrix, toleranced number, toleranced number interval, toleranced number vector, sparse toleranced number vector, toleranced number matrix or sparse toleranced number matrix.
Example:
Function: \(U(t)\) with \(\{U\}\) in V, \(\{t\}\) in s
Parameters: \(U_0\) in V with \(U_0=3.3\,\text{V}\)

<SymbolicFunction>
<SymbolicFunctionTemplate Symbol="U">
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">volt</mml:csymbol>
</mml:math>
</Unit>
<Arguments>
<ArgumentWithUnit Symbol="t">
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">second</mml:csymbol>
</mml:math>
</Unit>
</ArgumentWithUnit>
</Arguments>
<Parameters>
<ParameterWithUnit Symbol="U0" TeX="U_0">
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">volt</mml:csymbol>
</mml:math>
</Unit>
</ParameterWithUnit>
</Parameters>
<mml:math>
<mml:ci>U0</mml:ci>
</mml:math>
</SymbolicFunctionTemplate>
<ParameterValues>
<ParameterValueMagnitude Symbol="U0">
<SNumber>3.3</SNumber>
</ParameterValueMagnitude>
</ParameterValues>
</SymbolicFunction>
Validation:
This type is validated using the XML Schema file.
Attention
- See Symbolic Function Templates for details about validation of
<SymbolicFunctionTemplate>elements. - See Units, Unit Vectors, Sparse Unit Vectors, Unit Matrices and Sparse Unit Matrices for details about validation of
<Unit>,<UnitVector>,<UnitSparseVector>,<UnitMatrix>and<UnitSparseMatrix>elements. - See Numbers, Number Intervals, Number Interval Vectors, Number Vectors, Sparse Number Vectors, Number Matrices, Sparse Number Matrices, Toleranced Numbers, Toleranced Number Intervals, Toleranced Number Vectors, Sparse Toleranced Number Vectors, Toleranced Number Matrices and Sparse Toleranced Number Matrices for details about validation of
<ParameterValueMagnitude>elements.
Attention
- It is not validated whether parameters with the specified symbols exist in the symbolic function template.
- It is not validated whether values for all parameters of the symbolic function template have been specified.
Table Functions¶
Formal definition (auto-generated documentation based on XSD file).
Table functions describe mathematical functions in terms of their value table that includes all points for which the function is defined. They are useful for defining histograms. The domain and codomain of a table function are implicitly specified by the units of the function value and its arguments.
- Attributes:
- Symbol [xsd:string] – Function symbol
- TeX [xsd:string] (optional) – LaTeX function symbol
- Value:
- Unit (only if the following vector is not a string vector) – Unit of the function value
- *Vector* – Vector of function values; can be a string vector, sparse string vector, number vector, sparse number vector, number interval vector, toleranced number vector, or sparse toleranced number vector.
- Arguments:
- Argument (1..∞):
- Attributes:
- Symbol [xsd:string] – Function symbol
- TeX [xsd:string] (optional) – LaTeX function symbol
- Unit (only if the following vector is not a string vector) – Unit of the function argument
- *Vector* – Vector of function argument values; can be a string vector, sparse string vector, number vector, sparse number vector, number interval vector, toleranced number vector, or sparse toleranced number vector.
The given unit applies to all elements of the corresponding vector. All vectors must have the same number of elements.
Example 1:
A histogram is given by the following table:
| Temperature | Duration |
|---|---|
| -40°C … 10°C | 170 h |
| 10°C … 45°C | 500 h |
| 45°C … 105°C | 2000 h |
<TableFunction Symbol="t">
<Value>
<Unit>
<mml:math>
<mml:csymbol cd="SIUsed_OffSystemUnits1">hour</mml:csymbol>
</mml:math>
</Unit>
<NumberVector>
<SNumber>170</SNumber>
<SNumber>500</SNumber>
<SNumber>2000</SNumber>
</NumberVector>
</Value>
<Arguments>
<Argument Symbol="I">
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">degree-Celsius</mml:csymbol>
</mml:math>
</Unit>
<NumberIntervalVector>
<NumberInterval>
<LowerBound BoundType="closed">
<SNumber>-40</SNumber>
</LowerBound>
<UpperBound BoundType="closed">
<SNumber>10</SNumber>
</UpperBound>
</NumberInterval>
<NumberInterval>
<LowerBound BoundType="closed">
<SNumber>10</SNumber>
</LowerBound>
<UpperBound BoundType="closed">
<SNumber>45</SNumber>
</UpperBound>
</NumberInterval>
<NumberInterval>
<LowerBound BoundType="closed">
<SNumber>45</SNumber>
</LowerBound>
<UpperBound BoundType="closed">
<SNumber>105</SNumber>
</UpperBound>
</NumberInterval>
</NumberIntervalVector>
</Argument>
</Arguments>
</TableFunction>
Example 2: Electric vehicle charging/battery management profile from AEC-Q100 Appendix 7 Extended Lifetime proposal
| Temperature Ta [°C] | Duration [h] |
|---|---|
| -40 | 200 |
| -30 | 300 |
| -20 | 600 |
| -10 | 1100 |
| 23 | 1500 |
| 45 | 8350 |
| 60 | 14000 |
| 70 | 8000 |
| 80 | 2800 |
| 90 | 1800 |
| 100 | 800 |
| 110 | 250 |
| 115 | 120 |
| 120 | 100 |
| 125 | 80 |
<TableFunction Symbol="t">
<Value>
<Unit>
<mml:math>
<mml:csymbol cd="SIUsed_OffSystemUnits1">hour</mml:csymbol>
</mml:math>
</Unit>
<NumberVector>
<SNumber>200</SNumber>
<SNumber>300</SNumber>
<SNumber>600</SNumber>
<SNumber>1100</SNumber>
<SNumber>1500</SNumber>
<SNumber>8350</SNumber>
<SNumber>14000</SNumber>
<SNumber>8000</SNumber>
<SNumber>2800</SNumber>
<SNumber>1800</SNumber>
<SNumber>800</SNumber>
<SNumber>250</SNumber>
<SNumber>120</SNumber>
<SNumber>100</SNumber>
<SNumber>80</SNumber>
</NumberVector>
</Value>
<Arguments>
<Argument Symbol="Ta" TeX="T_a">
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">degree-Celsius</mml:csymbol>
</mml:math>
</Unit>
<NumberVector>
<SNumber>-40</SNumber>
<SNumber>-30</SNumber>
<SNumber>-20</SNumber>
<SNumber>-10</SNumber>
<SNumber>23</SNumber>
<SNumber>45</SNumber>
<SNumber>60</SNumber>
<SNumber>70</SNumber>
<SNumber>80</SNumber>
<SNumber>90</SNumber>
<SNumber>100</SNumber>
<SNumber>110</SNumber>
<SNumber>115</SNumber>
<SNumber>120</SNumber>
<SNumber>125</SNumber>
</NumberVector>
</Argument>
</Arguments>
</TableFunction>
Validation:
This type is validated using the XML Schema file.
Attention
- See Units for details about validation of
<Unit>elements. - See String Vectors, Sparse String Vectors, Number Vectors, Sparse Number Vectors, Number Interval Vectors, Toleranced Number Vectors, and Sparse Toleranced Number Vectors for details about validation of
<Value>and<Argument>elements.
Attention
- It is not validated whether all vectors have the same number of elements.
Transformed Functions¶
Formal definition (auto-generated documentation based on XSD file).
An existing function \(f(x_1, \ldots, x_n)\) can be transformed by preprocessing one or more of its arguments, postprocessing its value, or both. Preprocessing and postprocessing are defined using a transformation formula or function (symbolic, table, or another transformed function). The combination of preprocessing and postprocessing results in a transformed function
Postprocessing uses a value transformation formula/function \(v(z)\) that must refer to a single argument \(z\) and results in the expression \(v(f(x_1, \ldots, x_n))\). Additionally, when using a value transformation function \(v(z)\), the unit of that argument \(z\) must also be the same as the unit of the value of the original function: \([z] = [f]\). Clearly, the unit of the transformed function is the unit of the value transformation formula/function \(v(z)\). While a function defines this unit directly, the unit of a formula has to be derived from the unit of the original function.
Each argument \(x_i\) of the original function can be preprocessed using an argument transformation formula/function \(a_i(x_1, \ldots, x_n)\). Corresponding formulas and functions \(a_i\) must refer to the same number of arguments than the original function and their units must match as well. The (derived) unit of argument transformation formulas/functions must be the same as the unit of the original function argument: \([a_i] = [x_i]\).
- Attributes:
- Symbol [xsd:string] – Function symbol of the transformed function
- TeX [xsd:string] (optional) – LaTeX function symbol
- *Function* – Original function \(f(x_1, \ldots, x_n)\); can be a symbolic function, table function, or another transformed function.
- Transformation:
- ArgumentTransformations (optional):
- ArgumentTransformation (\(1..n\)):
- Attributes:
- Symbol [xsd:string] – Symbol \(x_i\) of the argument of the original function that will be transformed.
- *Formula/Function* – Formula or (symbolic, table, or transformed) function \(a_i(x_1, \ldots, x_n)\) that defines the transformation. Requirement: \([a_i] = [x_i]\).
- ValueTransformation (optional):
- *Formula/Function* – Formula or (symbolic, table, or transformed) function \(v(z)\) that defines the transformation. Requirement: \([z] = [f]\).
Example 1:
Based on the function \(U(t)=3.3\,\text{V}\), we define a transformed function \(U'(t) = -U(t)\)
<TransformedFunction Symbol="U-trans">
<SymbolicFunction>
<SymbolicFunctionTemplate Symbol="U">
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">volt</mml:csymbol>
</mml:math>
</Unit>
<Arguments>
<ArgumentWithUnit Symbol="t">
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">second</mml:csymbol>
</mml:math>
</Unit>
</ArgumentWithUnit>
</Arguments>
<Parameters>
<ParameterWithUnit Symbol="U0" TeX="U_0">
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">volt</mml:csymbol>
</mml:math>
</Unit>
</ParameterWithUnit>
</Parameters>
<mml:math>
<mml:ci>U0</mml:ci>
</mml:math>
</SymbolicFunctionTemplate>
<ParameterValues>
<ParameterValueMagnitude Symbol="U0">
<SNumber>3.3</SNumber>
</ParameterValueMagnitude>
</ParameterValues>
</SymbolicFunction>
<Transformation>
<ValueTransformation>
<Formula>
<FormulaTemplate Symbol="neg">
<Arguments>
<Argument Symbol="x"/>
</Arguments>
<mml:math>
<mml:apply>
<mml:csymbol cd="arith1">unary_minus</mml:csymbol>
<mml:ci>x</mml:ci>
</mml:apply>
</mml:math>
</FormulaTemplate>
</Formula>
</ValueTransformation>
</Transformation>
</TransformedFunction>
Example 2:
Based on the function \(U(t)=3\,\frac{\text{V}}{\text{s}}\cdot t\), we define a transformed function \(U'(t) = U(t-2s)\) that introduces a delay of \(2\,\text{s}\).
<TransformedFunction Symbol="U-trans">
<SymbolicFunction>
<SymbolicFunctionTemplate Symbol="U">
<Unit>
<mml:math>
<mml:csymbol cd="SI_NamedDerivedUnits1">volt</mml:csymbol>
</mml:math>
</Unit>
<Arguments>
<ArgumentWithUnit Symbol="t">
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">second</mml:csymbol>
</mml:math>
</Unit>
</ArgumentWithUnit>
</Arguments>
<Parameters>
<ParameterWithUnit Symbol="m">
<Unit>
<mml:math>
<mml:apply>
<mml:csymbol cd="arith1">divide</mml:csymbol>
<mml:csymbol cd="SI_NamedDerivedUnits1">volt</mml:csymbol>
<mml:csymbol cd="SI_BaseUnits1">second</mml:csymbol>
</mml:apply>
</mml:math>
</Unit>
</ParameterWithUnit>
</Parameters>
<mml:math>
<mml:apply>
<mml:csymbol cd="arith1">times</mml:csymbol>
<mml:ci>m</mml:ci>
<mml:ci>t</mml:ci>
</mml:apply>
</mml:math>
</SymbolicFunctionTemplate>
<ParameterValues>
<ParameterValueMagnitude Symbol="m">
<SNumber>3</SNumber>
</ParameterValueMagnitude>
</ParameterValues>
</SymbolicFunction>
<Transformation>
<ArgumentTransformations>
<ArgumentTransformation Symbol="t">
<Formula>
<FormulaTemplate Symbol="delay">
<Arguments>
<Argument Symbol="t"/>
</Arguments>
<Parameters>
<Parameter Symbol="d"/>
</Parameters>
<mml:math>
<mml:apply>
<mml:csymbol cd="arith1">minus</mml:csymbol>
<mml:ci>t</mml:ci>
<mml:ci>d</mml:ci>
</mml:apply>
</mml:math>
</FormulaTemplate>
<ParameterValues>
<ParameterValue Symbol="d">
<Quantity>
<SNumber>2</SNumber>
<Unit>
<mml:math>
<mml:csymbol cd="SI_BaseUnits1">second</mml:csymbol>
</mml:math>
</Unit>
</Quantity>
</ParameterValue>
</ParameterValues>
</Formula>
</ArgumentTransformation>
</ArgumentTransformations>
</Transformation>
</TransformedFunction>
Validation:
This type is validated using the XML Schema file.
Attention
- See Formulas, Symbolic Functions, and Table Functions for details about validation of these elements.
Attention
- It is currently not validated whether formulas and functions have the correct number of arguments and the correct units.
References¶
To avoid the need for a repeated definition of the same element, already defined elements can be referenced.
For this purpose, a unique “Id” attribute can be specified for all elements.
Later, these elements can be referenced using special reference elements that have the same name with the ending “Ref”.
For example, <String> elements are referenced using <StringRef> elements.
These reference elements have a single attribute “Ref” whose value is the Id of the referenced element.
Wherever a certain element is expected, a corresponding reference can be used.
Example:
<String Id="my-string-01">Hello World</String>
<StringRef Ref="my-string-01"/>
Validation:
All <*Ref> elements are validated using the XML Schema file.
Schematron rules ensure that all IDs refer to the correct element type, e.g., only IDs of <String> elements can be referenced by <StringRef> elements.
